Binary Search Tree
A tree is a collection of nodes , where every node can have one or more child nodes . Root node is present at the top of the tree.
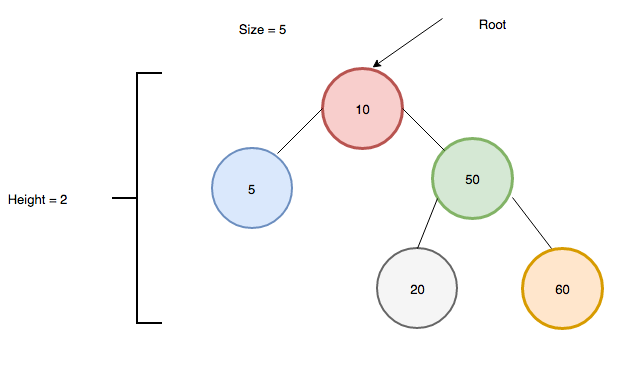
A binary search tree is a tree where each node can have 0 , 1 or 2 children.
For each node the element on its left will be less than the current node and the element on the right will be greater than the current node.
- A tree is a full binary tree if every node has exactly 2 children and all the leaf nodes are at the same level
- The number of nodes in a full binary tree is 2^ (h + 1) - 1 . Since there are h levels we need to add the nodes at all levels [2^0 + 2^1 + 2^2 + ...2^h] which is 2^ (h + 1) - 1
- There are 6 different ways in which a tree can be traversed , but since the classification depends on the position of the current node , this resolves to 3 ways
- Preorder (DLR) traversal
- Inorder (LDR) traversal
- Postorder (LRD) traversal
- There is another traversal called Level Order Traversal which drew its inspiration from Breadth First Search